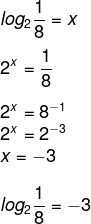O logaritmo é a uma operação matemática usada para se descobrir o expoente que uma determinada base deve ter para resultar em uma potência.
Definição de logaritmo
O logaritmo é uma operação matemática. Ela está relacionada de forma direta com as equações exponenciais. Sendo que o intuito é encontrar o expoente que faz com que a base seja igual ao que chamamos de logaritmando.
Na prática, são resolvidas as equações exponenciais. Contudo, com essa operação surgem propriedades importantes que ajudam nas resoluções.
Desse modo, para resolvê-lo, é muito importante ter o domínio da operação e das propriedades existentes para ele. Sendo que elas se parecem muito com as propriedades das potências.
Além disso, para que essa operação seja bem definida, existem algumas restrições para o valor da base e do logaritmando chamadas de condição de existência.
Enfim, chamamos de logaritmo de a na base b, representado por logab, o valor x, tal que a elevado a x seja igual a b.
Por exemplo, ao escrevermos log28 (lê-se logaritmo de 8 na base 2), estamos procurando o número a que devemos elevar o 2 para que a resposta seja igual a 8.
Log28 = 3, pois 2³ = 8.
No geral, a operação é definida por:
x → logaritmo
b → base
a → logaritmando
Atenção: Quando não escrevemos a base, ela é sempre igual a 10, ou seja, Log a (lê-se logaritmo de a na base decimal).
Casos particulares de logaritmos
Agora que você conhece a definição, vamos analisar alguns casos particulares.
- logb1 = 0, pois a0 = 1.
Todo número elevado a 0 é igual a 1. Portanto, o logaritmo de 1 em qualquer base é sempre igual a 0.
Exemplo numérico: log81 = 0, pois 80 = 1.
- logbb = 1, pois b1 = b.
Todo número elevado a 1 é ele mesmo. Sendo assim, o logaritmo de base e logaritmando iguais são sempre iguais a 1.
Exemplo numérico: log55 = 1, pois 5¹ = 5.
- Se logba = logbc, então a = c, pois bx = a e também bx = c.
Dois logaritmos de mesma base são iguais se, e apenas se, o logaritmando for igual.
Exemplo numérico: Sabendo que logb8 = logba, então a = 8.
- logbbn = n, pois, pela definição, bn = bn.
Esse caso é uma aplicação da definição, já que a base levada ao logaritmo é igual ao logaritmando.
Exemplo numérico: log22³ = 3, pois 2³ = 2³.
Condição de existência
Existem algumas restrições sobre os valores da base e do logaritmando.
Em síntese, a base de um logaritmo sempre deve ser um número positivo e diferente de 1, e o logaritmando deve ser sempre um número positivo. Na forma algébrica, temos:
logba
Sendo que a e b são números reais, tal que: a > 0 e b > 0 e b ≠ 1.
Como resolver
Alguns logaritmos podem ser resolvidos de forma direta, somente com a definição. Mas existem outros que exigem o domínio de equações exponencias.
Além disso, se for preciso, deve-se fazer a consulta da tabela de logaritmos decimais para saber o valor que não conseguimos calcular com base em uma equação exponencial.
Exemplo 1
Para calcular log3243, siga o passo a passo:
1º passo
Aplique a definição para transformar o logaritmo em uma equação exponencial.
Seja log3243 = x, então 3x = 243.
2º passo
Iguale as bases quando possível.
3x = 35 → x = 5
Exemplo 2
Vamos calcular o logaritmo a seguir.
Tendo como base os dois passos do exemplo anterior, é preciso aplicar a definição e tentar igualar as bases. Sendo assim:
Propriedades dos logaritmos
Como existem casos onde a aplicação da definição não é suficiente para resolvê-los, foram desenvolvidas certas propriedades que facilitam essa resolução.
Desse modo, dominar essas ferramentas é indispensável para a resolução dos problemas sobre esse tema e para usar logaritmos para solucionar equações exponenciais de bases diferentes.
Por exemplo, vamos considerar X e Y dois números reais positivos e diferentes de 1 para todas as propriedades seguintes:
1ª propriedade: produto
logb(X.Y) = logbX+ logbY
Em resumo, o logaritmo de um produto pode ser separado na adição do logaritmo de mesma base de cada um dos fatores.
2ª propriedade: quociente
Essa propriedade se parece bastante com a anterior. Dessa forma, o quociente pode ser separado com a subtração dos logaritmos de mesma base do numerador pelo denominador, nessa ordem.
3ª propriedade: potência
logbXn = n . logbX
Por fim, sempre que tiver um expoente no logaritmando, o logaritmo de uma potência será igual à multiplicação desse expoente pelo logaritmo.
Enfim, gostou do texto? Pois saiba que aqui no site Conhecimento Científico, existem vários outros textos que você pode gostar.
Por exemplo, você pode aprender como calcular a probabilidade. Ou ainda, qual é a diferença entre mediana, moda e média.
Fonte: Info Escola, Wikipédia, Toda Matéria, Só Matemática, Mundo educação, Brasil Escola, Blog do Enem, Cola da Web.