O seno em um triângulo retângulo
Em resumo, o seno representa a razão do ângulo entre o cateto oposto a esse ângulo e a hipotenusa.
Dessa maneira, para que a razão seja encontrada é necessário utilizar a seguinte fórmula que representa o cateto oposto sobre a hipotenusa. Desse modo, temos: sen(α) = cateto oposto a α / hipotenusa
Além disso, um ângulo do retângulo triângulo é denominado de agudo. No entanto, dentro do triângulo também existem os ângulos notáveis, representados por 30°, 45° e 60°.

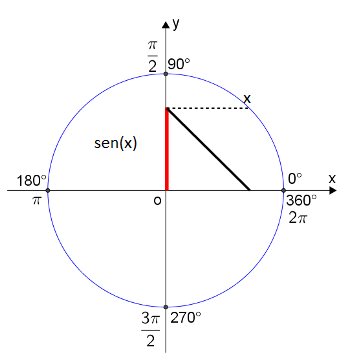
Sendo assim, os ângulos notáveis ficam dispostos no círculo trigonométrico, onde seno sempre ficará sobre o eixo das ordenadas (y).
Dessa forma, contando que o círculo possui 4 quadrantes, o seno será positivo no 1º e 2º e negativo no 3º e 4º quadrantes.
Por fim, em relação aos ângulos notáveis, cada um possui um valor dentro do círculo trigonométrico. Dessa maneira, o seno de 30º representa 1/2; 45º equivale a √2/2 e 60º possui valor de √3/2.
Seno dos ângulos notáveis
Em síntese, os ângulos notáveis são aqueles calculados com mais frequência (30°, 45° e 60°).
sen (30°) = (x/2)/x = x/2 . 1/x = 1/2
sen (60°) = h/x
Em contrapartida, para determinar o valor do seno de um ângulo de 45°, podemos usar o quadro abaixo, tendo como base um quadrado de lado x:

Desse modo, o cálculo deve ser feito da seguinte maneira:
sen (45º) = x/(xv2) = 1/v2
sen (45º) = 1/v2 . v2/v2 = v2/2
Enfim, a tabela abaixo serve como base dos cálculos dos senos dos ângulos de 30º, 45º e 60º.
| 30º | 45º | 60º | |
| Sen | 1/2 |
v2/2
|
v3/2
|
Função
Em resumo, a função do seno pode ser definida como: f(x)=sen(x)
Além disso, no círculo trigonométrico é possível verificar a função seno como o intervalo [-1,1].
Dessa forma, os valores que o seno pode assumir para qualquer valor x variam entre -1 e 1. Ou seja, podemos exemplificar isso como: -1 = sen(x) = 1, para todo x real.
Por fim, vale notar que o seno de um ângulo sempre estará sob o eixo das ordenadas (y). Sendo assim, o seno de um ângulo será sempre positivo no 1º e 2º quadrantes e negativo no 3º e 4º quadrantes.
Gráfico
A tabela abaixo representa a função:
| X | f(x) = sen (x) |
| 0 | 0 |
| p/2 | 1 |
| p | 0 |
| 3p/2 | -1 |
| 2p | 0 |
Portanto, com base nessa tabela, temos o seguinte gráfico:

Exercícios
Por fim, teste seus conhecimentos com as questões abaixo:
UFPR
Calcule o seno do maior ângulo de um triângulo cujos lados medem 4,6 e 8 metros.
- √15/4
- 1/4
- 1/2
- √10/4
- √3/2
UECE
O menor lado de um paralelogramo, cujas diagonais medem 8√2 m e 10 m e formam entre si um ângulo de 45º, mede:
- √13 m
- √17 m
- 13√2 / 4 m
- 17√2 / 5 m
Enem de 2011
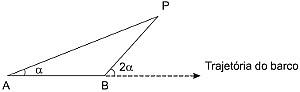
Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual α fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B da praia, no entanto sob um ângulo visual 2α. A figura ilustra essa situação:
Suponha que o navegante tenha medido o ângulo α = 30° e, ao chegar ao ponto B, verificou que havia percorrido a distância AB = 2 000 m. Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será:
a) 1000 m.
b) 1000√3 m.
c) 2000 √3/3 .
d) 2000 m.
e) 2000√3 m.
Gabarito
UFPR: O correto é a alternativa A)
UECE: O certo é a opção B)
Enem de 2011: O certo é A)
Fontes: Toda Matéria, Info Escola e, por fim, Matemática Básica.
Bibliografia:
- DANTE, Luiz Roberto. Matemática: contexto & aplicações 2 ed São Paulo: Ática, 2013.
- IEZZI, Gelson. Fundamentos de Matemática Elementar Trigonometria Vol 3 São Paulo: Atual, 1995.
- GOUVEIA, Rosimar. Seno, Cosseno e Tangente [20–] Acesso em: 19 março 2020.
- Seno, Cosseno e Tangente no Enem. Brasil escola Acesso em 06 de dezembro de 2022.